Easy-To-Use Computer Modules Are Bringing The Math Behind Space-Time To Everyday Problems.
It is with some glee that we storytellers watch the numeric elite bumble with the nasty mathematical concept called a tensor. If a tensor sounds like something you might take a Tylenol or Advil to get rid of -- as in, “Wow I have a heck of a tensor headache,” -- you’re not far from the stress these gnarly concepts place on the average analogy-challenged mathematician.
“Tensor analysis is the type of subject that can make even the best of students shudder,” writes Joseph C. Kolecki, of NASA’s Glenn Research Center in Cleveland, in his paper, An Introduction to Tensors For Students of Physics and Engineering.
Tensors are part of the family of logical hardware used in complex calculations found in construction, physics and more and more, machine learning. In these times of artificial intelligence, tensors play a critical role in automating how objects, forces and functions are used -- and abused -- by computers. It is no accident that Google’s Machine Learning language is dubbed TensorFlow. And open-source machine learning languages like PyTorch have serious tensor-based elements.
We are by no means tensor bigots here at The Trusted Face. This past week, we began deploying our own tensors, as we begin to get serious about writing the software that tells truth from fiction for any video on the Web. What's been intriguing for us, when dealing with tensors, is how computer learning is no longer merely a computational problem, but a storytelling problem.
And as narratives go, tensors are not much trouble indeed. All one needs, is a math nerd with a handle on the basic principles, as broken out in lists like Deep Learning with PyTorch: A 60 Minute Tutorial. And then a feel for a good story and a sense for the right, readily-available computer tools. Just about anybody can put tensors to work to solve complex problems.
We are doing now. And we are really old people with theater and physical therapy degrees. If we can handle tensors, so can you.
Learning To Speak In The Proper "Tensor."
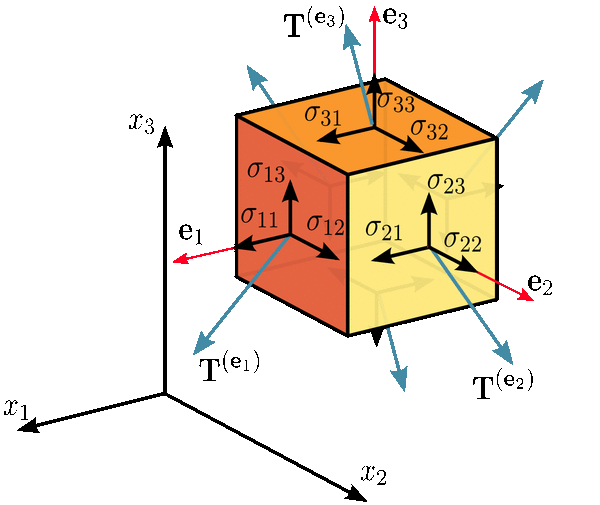
Let’s get the math jargon out of the way: A tensor is an abstraction of something called a matrix, which is, in turn, an abstraction of something called a vector, which is, in turn, an abstraction if something called a scalar. It sounds all tricky and "mathish." But don't be intimidated. Tensors are basically like blues music. It's the same three cords, over and over: Basic numbers that count something; a second number that scales that first number with additional information; a third a number that carries the other two numbers, usually in a definite direction, into something called a vector or a gradient. And then cool blusie part happens, when all three of those elements are suspended into a three-dimensional conceptual erector set of vectors, scalars, and numbers called a matrix.
Just like that cool blues E7 chord, that every wanna-be guitar player learns, that kind of tensions the music, a tensor adds a dimensional twist to the matrix of scalers and vectors to add additional context and capabilities to the story scientists are trying to tell. To demonstrate, let's make a tensor about the zippy new lunar lander announced by Blue Origin, Jeff Bezos’ hobby rocket company with plans to fly to the moon in the next few years.
- Step 1: Count One Thing With One Number: All tensors originate with a single number used to define, count or otherwise measure one specific thing. In Blue Origin’s case, that thing is the Blue Moon Lander. Mathematically speaking, this one lander is described, or abstracted by, the number 1. Isn't math glorious?
- Step 2: "Scale" That First Thing With A Second Number: Our Blue Moon lunar lander won’t get to the moon, if it sits on its numeric butt doing nothing. It needs to move. So, we will need to add a second number, or a velocity, to our first number. This second value is generically known as a scalar. In this case, our velocity scaler is close to 24,500 miles per hour; that's the speed objects travel on their way to the moon. Our first number counts the lander. Our second number scales how fast that one lander is going. Why math is given the mystic it is given, heaven only knows.
- Step 3: Carry Those Scaled Two Things As A Third "Vector." Our one lander, traveling at 24,500 mph doesn’t tell us where that lander is going. For that, we need a third number that gives us a sense of the direction that will lead that lander to the moon. Relative to our office in suburban New York City, at about 11 a.m. on the day we're writing this story, the moon is roughly located 240 degrees. To describe that direction, we crib the Latin verb "to carry," and make something called a vector that accurately measures where the Blue Origin Lander is headed, how fast it is going and in what direction.
- Step 4: Install Your Scalers and Vectors into a Matrix: Once we have our one lander, moving out our 24,500 miles per hour, heading at 240 degrees, we can set up the square scaffolding of a numbers, expressions or other values organized in conceptual rows or columns. Ever seen the really strange tridimensional chess set that Commander Spock plays in the really old Star Treks? Matrices are like that, but made of hard-to-visualize things like scalars and vectors. Just because you can't see math, does not mean it's impossible to understand.
Shaping Our Vector with Some Heavy “Tensoring."
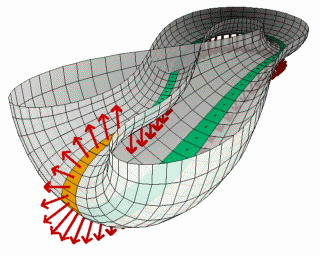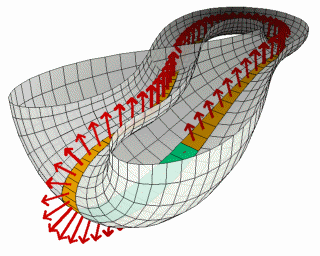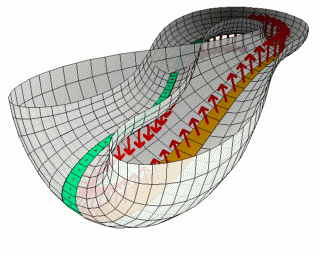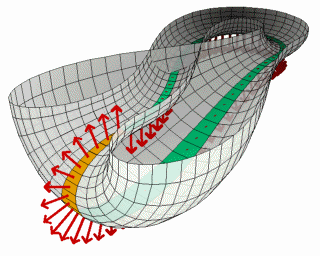
Now comes the stress and strain of tensors: To tell the deeper story of our one lander, traveling at 24,500 mph in a direction of 240 degrees, we need to account for how the Earth and the Moon move as the lander travels. But here is the relativistic thing: Space and time are warped by the gravity of both planets. Exactly how gravity that bend that space and time, the scaler, vector and matrix that describes the path of our Blue Origin lander must be tensioned by some serious tensor math. For example, Gron and Hervik’s often-quoted breakdown of Einstein's General Theory of Relativity, mentions the concept of the tensor 620 times.
And the language used to summarize even an arbitrary tensor, much less the really challenging ones, will make your head spin. Take a look at this list below.
eÆ Partial derivative
rÆ Covariant derivative
$X Lie derivative with respect to X
D Exterior derivative operator
Dy Codifferential operator
§ Covariant Laplacian
≠ Tensor product
^ Wedge productAnd here's a serious simplified visualization of where all those forces are headed: